Terre de l'homme

https://www.rhune.com/fr/sommet-de-la-rhune/panorama-360/

Quand j'étais un pré-adolescent, je fus fasciné par le champ de vision de la Rhune qui, du haut de ses 905 mètres, cherche dans le Golfe de Gascogne sa ligne d'horizon à 107 km. Sur ce sommet dominant Ascain, si la transparence du ciel est de la partie, on aperçoit les hauteurs du Monte Igueldo à Saint-Sébastien.

C'est toujours avec une forme de saisissement, voire d'émerveillement, que l'on observe l'horizon. Chaque jour, de ma chaumière, je porte mon regard sur Pessarni, Le Bloy et Tourneguil en découvrant le faîte de son château d'eau. 

Merci Pythagore !

Pythagore est un réformateur religieux et philosophe pré-socratique qui serait né aux environs de 580 av. J.-C. à Samos, une île de la mer Égée au sud-est de la ville d'Athènes ; on établit sa mort vers 495 av. J.-C., à l'âge de 85 ans. Il aurait été également mathématicien et scientifique selon une tradition tardive. Wikipédia   Son théorème est-il authentique ou apocryphe...  gardons-nous d'affirmer. En tout état de cause, il est parvenu jusqu'à nous comme étant son énonciation.

Bien des années après notre scolarité, même si elle fut, comme celle de votre serviteur, désastreuse, pitoyable et lamentable, tous ou à peu près, nous gardons en mémoire l'incontournable théorème de Pythagore.

C'est en prenant appui sur cet énoncé que l'on admet ou que l'on conteste le champ de portée de la ligne d'horizon.

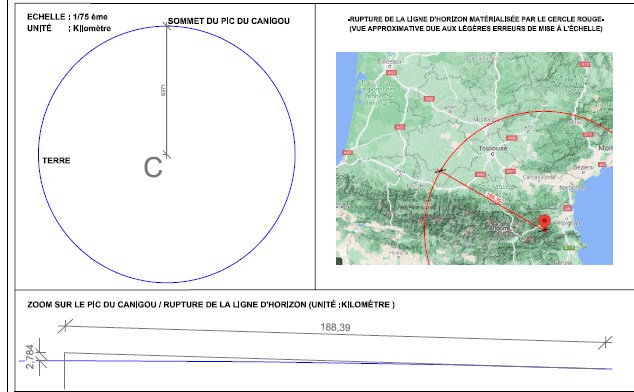
Faisons simple et cherchons la ligne d'horizon à partir du Canigou, alt 2 785 m. Toujours pour faire simple, on va admettre que le rayon de la Terre est de 6 371 km, il faut bien considérer que la Terre n'est pas une sphère parfaite. On va chercher à quelle distance on perd la ligne d'horizon. 

√ (6371 + 2.785²) – (6371²) = 188,3991 km

Vérifions la réciprocité

√ (188,3991² + 6371²) = 6 373,785 – 6371 = 2,785 km

Le Canigou culmine bien à 2 785 m.

En admettant le rayon de la Terre à 6 371 km, le sommet du Canigou, lui, est 6 373,784 km du centre de notre planète.

Constatons la justesse de Pythagore.

6371² = 40 589 641

188,3991² = 35 494,22088

L'addition de 40 589 641+ 35 494,22088 = 40 625 135,22088

Extrayons la √ de 40 625 135,22088 et nous obtenons 6 373,7849995807044009034028603552

 6 373,7849995807044009034028603552 étant l'hypoténuse du triangle, on constate donc bien l'exactitude du triangle.

_____________________

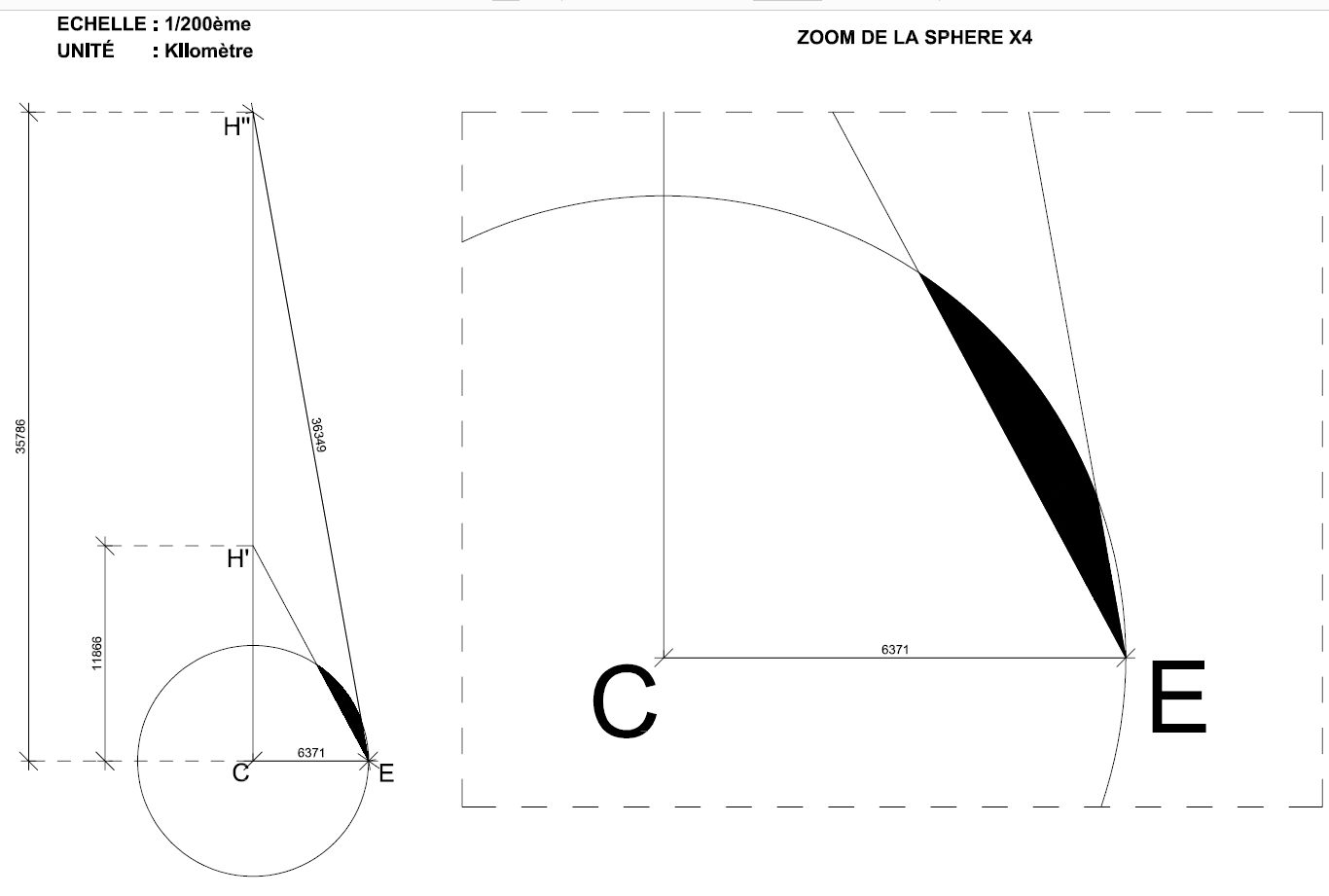
Année olympique oblige, appuyons-nous sur la devise " Plus vite, Plus Haut, Plus Fort ..." et cherchons l'orbite géostationnaire.

L'orbite géostationnaire,  qu'est-ce que c'est ?

Cette orbite abrégée GEO (geostationary orbit) est une orbite circulaire autour de la Terre caractérisée par une inclinaison orbitale nulle (donc une orbite dans le plan équatorial), et une période orbitale (durée d'une orbite) égale à la période de rotation de la Terre. Un objet placé sur une orbite géostationnaire reste en permanence au-dessus du même point de l'équateur.

L'orbite géostationnaire autour de la Terre se situe à une altitude de 35 786 km au-dessus du géoïde terrestre ; on parle couramment de satellites à 36 000 km.

CLIQUEZ SUR LE GRAPHIQUE

Croquis établissant la nécessité de se placer très haut pour pratiquement apercevoir la moité de La Terre. Contribution graphique de notre jeune contributaire Sylvain Bouyssou.

Notre globe ne manque pas de points de vue extraordinaires. Citons la Dune du Pyla. De là, quand les conditions sont idéales, les Pylatais aperçoivent les Pyrénées distantes d'environ 200 km. Les belvédères de la Côte d'Azur surprennent la Corse, également distante de 200 km.

Des reliefs entourant le Détroit de Béring, large de 90 km, virtuellement, dans les meilleures conditions, on peut passer des extrémités sibériennes de l'Asie à celles alaskiennes, tout comme des reliefs de l'isthme de Panama, la projection visuelle atteint les deux océans ; mais, restons bien chez nous et contentons-nous de remarquer, de Biron, la barrière pyrénéenne ou, de la Borne 120, au nord de Sarlat, de surprendre le magnifique panorama quercyno-limousin. Enfin, du haut du Phare de Cordouan, cernons la spectaculaire jonction de la Gironde et de l'Atlantique.

P-B F