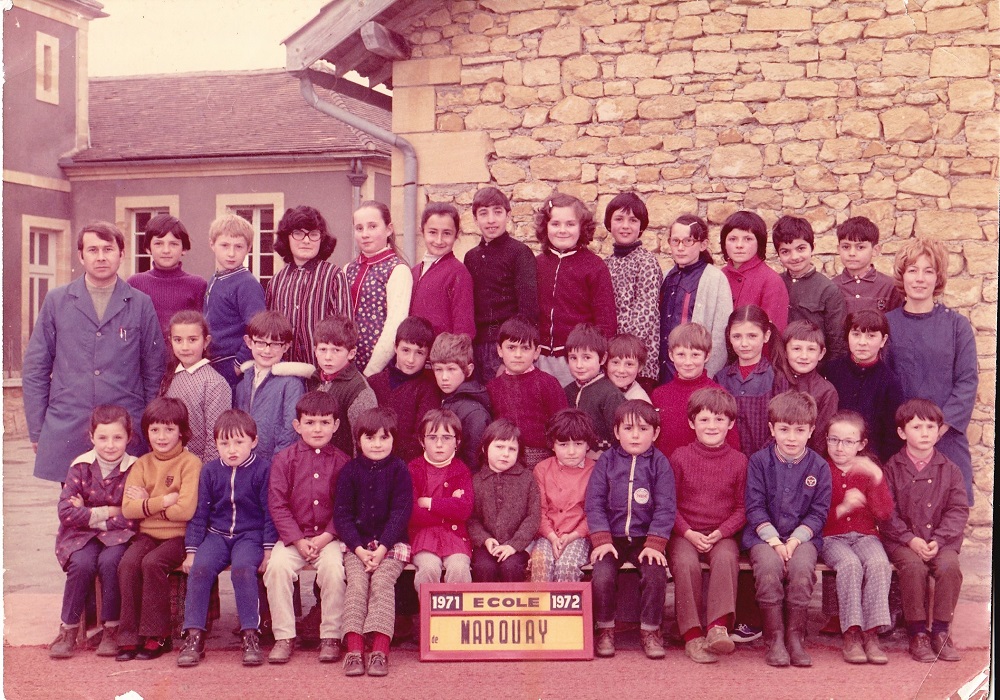Terre de l'homme

Qu'est ce qu'un dénominateur commun.

Le sens du dénominateur commun est presque un paradoxe. En mathématique, c'est le diviseur commun de plusieurs fractions. Dans la vie sociétale, il désigne l'élément commun à plusieurs personnes. Le dénominateur commun porte donc le sens de diviseur commun et de rassembleur sociétal.

Le dénominateur commun peut, tout à la fois, être positif ou négatif. Positivement, on peut dire "Les  médecins sont des piliers du corps médical", le corps médical étant, pour ces personnes, le dénominateur commun ; a contrario, négativement, disons, "les adeptes effrénés des voyages aériens, ou les sportifs pratiquant les sports d'hiver", ont pour dénominateur commun, l'inconscience d'hypothéquer l'avenir de leurs descendants.

Les écoliers marquayais apprenaient encore cette vieille méthode de conversion des fractions. Ces élèves ont eu la chance de rencontrer, pour l'initiation à la vie citoyenne, de sympathiques instituteurs Huguette et Georges Labrousse qui avaient vigoureusement banni la détestable pédagogie des enseignants revêches... voire "méphistophéliques".

Ils ont bien voulu, en témoignage d'amitié pour Terre de l'Homme,  nous envoyer une image de leur école primaire d'il y a... bientôt 40 ans. 

Revenons à l'école primaire d'antan.

Imaginez que vous ayez à apprécier, à la louche, dans une discussion ou un jeu 2/3 + 3/4. Vous trouverez certainement, en tâtonnant, même si vous avez perdu la méthode, que c'est la même chose que 8/12 + 9/12. Vous aurez donné à ces deux fractions, un dénominateur commun.

Si vous poussez plus loin, vous pourrez comparer ces deux fractions en estimant que 2/3 + 3/4, c'est exactement égal à 6/9 + 6/8. Là vous aurez trouvé le numérateur commun.

Si vous faites une règle de 3, vous trouverez que ces fractions dans les deux cas 66,6… %  et 75 %.

Une première remarque. Les fractions ayant un dénominateur commun, permettent des opérations telles que l'addition de 8/12 + 9/12, ce qui donne 17/12 soit 141,66… %. Des fractions avec un numérateur commun, n'autorisent aucune opération. Elles ne permettent que des comparaisons, bien sûr 6/9 est plus petit que 6/8. Le numérateur commun n'apporte donc pas grand-chose. On pourrait presque dire que c'est une "amusette" arithmétique.

Nous venons là de rechercher le dénominateur commun et le numérateur commun de deux fractions… la belle aventure ! Jadis, sur les bancs de l'école primaire, cette démarche intellectuelle était imposée aux élèves des cours moyens. Il leur était demandé de l'obtenir, sans tâtonner, en définissant la méthode imparable qui leur permettait d'obtenir ces résultats. Aujourd'hui, on peut estimer, à juste titre, que ce casse tête, qui torturait les esprits, sans être absurde, avait plus pour objectif une ouverture d'esprit arithmétique qu'une finalité pragmatique pour la vie courante ultérieure de ces élèves. On ne peut pas du tout affirmer que l'appropriation de cette règle ait permis à ces écoliers, dans le prolongement de leur vie citoyenne, de résoudre de nombreuses problématiques !

Il n'est pas du tout certain qu'un notaire, amené à diviser les tantièmes d'une succession compliquée, recoure au dénominateur commun de fractions.

Aujourd'hui, les esprits que l'arithmétique effraie, en ne voulant pas s'encombrer l'esprit, contournent la subtilité en pratiquant la proportionnalité. Ainsi ils trouveront que 2/3 c'est 66,66… % et 3/4 c'est 75 %, ce qui est fort juste et permet d'apprécier l'ordre de grandeur de ces fractions.

De nos jours, il n'est pas du tout certain que les étudiants, armés d'un riche cursus universitaire, aient une idée précise et certaine de la recherche arithmétique de dénominateur ou de numérateur commun. Heureusement, cela ne les empêche pas de progresser à pas de géants dans bien des domaines. De brillants matheux n'ont, hélas, cure de l'accord des participes passés. H₂SO₄ la formule chimique de l'acide sulfurique, tout comme HCl, formule brute de l'acide chlorhydrique, ne sont pas forcément indispensables et nécessaires sur les bancs d'une faculté de droit. Il paraît même permis de supposer que  parmi les docteurs es sciences mathématiques, on trouve, çà et là, de brillants universitaires qui soient dubitatifs sur un myriagramme et même qui aient besoin de quelques secondes pour définir un centiare, définition qui jadis devait jaillir spontanément des écoliers pour éviter l'ire de l'instituteur revêche.

Obtenir un dénominateur commun.

Partons de deux fractions ayant pour numérateurs et dénominateurs, des nombres premiers : 11/13 et 17/19.

La multiplication des dénominateurs 13 x 19 donnera 247. Ce sera le dénominateur commun.

Cherchons maintenant les numérateurs. Pour ce faire, nous multiplierons  11 x 19 et 17 x13. On obtiendra  209 et 221.

11/13 et 17/19 = 209/247 et 221/247.

Vérifions par la méthode de la règle de 3. Ces fractions donnent 84,61 % et 89,47 %.

Des fractions avec un dénominateur commun permettent au premier regard de voir laquelle est celle qui est la plus importante. On notera que l'addition de fractions ayant un dénominateur commun est possible.

Obtenir un numérateur commun.

Gardons toujours nos fractions constituées de nombres premiers : 11/13 et 17/19^ème.

Pour obtenir un numérateur commun, il faudra rechercher le produit de 11 x 17. On obtiendra donc 187.

Il faudra ensuite multiplier le numérateur 11 par le dénominateur 19 et ensuite 17 x 13. On obtiendra donc 187/221 et 187/209.

Le but de rechercher un numérateur commun est de mesurer l'ordre de grandeur des 2 fractions. Ainsi, on s'aperçoit que la seconde dégage un résultat plus important.

On notera que l'addition de fractions ayant un numérateur commun est impossible.

Cette manipulation, nous la vérifions par la règle de 3. On se rend compte que  11/13 = 187/221 et on trouve que cette fraction est égale 84,61 % tandis que 17/19 = 187/209 est égale à 89,47 %.

L'unique avantage de la fraction est d'illustrer des nombres entiers, la proportionnalité obtenue par la règle de 3, bien souvent, donne des produits irrationnels.

Les fractions sont parfois divisibles.

Prenons 26/4 cette fraction est égale à 13/2.

Si l'on est en présence de 2 fractions et que l'on tienne à garder le paramètre de dénominateur, ou de numérateur commun, il faut que l'ensemble des nombres soient réductibles par le même diviseur. Ainsi si l'on veut réduire 667/1679 et 667/1769, il faudra commencer par chercher le plus fort démultiplicateur commun à l'ensemble de ces nombres 1769, 1679 et 667.

Autrefois, on appelait PGCD, le plus grand commun diviseur. En divisant par le PGCD, tous les nombres de l'équation, on obtient les fractions les plus réduites.

En consultant la liste des nombres premiers, on constate qu'il n'y a aucune hypothèse de divisibilité pour 1769 avant d'atteindre 3538.  Par ailleurs, 1769 tout comme 1679 ne sont pas divisibles par 667,  on ne peut pas réduire cette fraction.

Attention, tous les nombres servant à concevoir des fractions doivent être des entiers, il ne peut y avoir de virgule.

Pierre Fabre